Phys345: Quantum Physics-1

Quantum Physics-I 量子物理-1, Fall 2011

Announcement:

Time: T1T2F1F2 Tue: 8:30-9:50 and Fri: 8:30-9:50
Classroom: Room 002, Physics

Lecturer: We-Fu Chang (張維甫)
e-mail: < wfchang_AT_phys_nthu_edu_tw >
Room618, ext 31111
Office Hour: Tue. 10:00-11:00, Fri. 10:00-11:00 (暫訂)

Tutorial section: Mon. 6-7pm, Thu. 7-8pm, R002

Prerequisite: 本課程適合大三（含）以上，修過理論力學及電磁學之同學選修.
You are expected to have the mechanics and Electromagnetism knowledge at the level of
sophomore.

Textbook: Griffith, Introduction to Quantum Mechanics, 2nd ed.

Recommedned References

R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles, 2nd ed.
R.P. Feynman, The Feynman lecture of Physics III
S. Gasiorowicz, Quantum Physics, 3rd ed.

Grading Policy: 30% Homework, 20% Midterm 1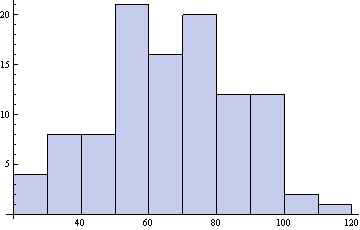

+20% Midterm 2

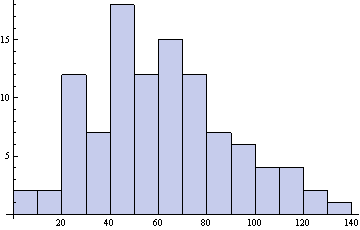, 30% Final

, 原始總分分佈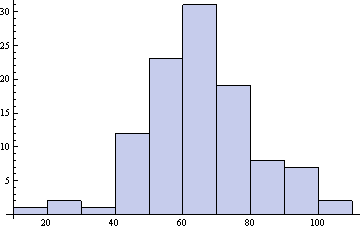

    (* Note: to pass this course, the sum of your two midterms and your final must be greater than 100.
      注意: 你的兩次期中考加期末考分數相加至少要有 100 分, 才有機會過關. )

TA:
許智婷 0910-765580 googoogoojube@gmail.com , R605
周明翰 0912-488767 mike23921887@hotmail.com, R510A
蔡松庭 0921-613548 e68482100@yahoo.com.tw , 同步輻射
Discuss with the TA if you have any question about your homework grading.

Homework:

( 注意: 不收遲交作業, 對抄襲或作弊零容忍 )
Doing the problem sets is an extremely important part of learning. You can't learn the subject by just listening to the lectures without working through things by yourself. They also contain some of the important topics that we won't be able to cover in class. You can discuss the problem sets with your classmates, but you are not allowed to copy other people's homework. Each of you is required to write up your own homework following your own understandings. Each problem set is due about one week after its assignment in class. The solutions will be given on this website immediately after the class on the due day and hence late submition will not be accepted.
So even if you couldn't finish you should turn in what you have done.
You should summit the HW to the TA's ahead of the deadline if for some reason you can't attend the class on the due day.

The following homework solutions are provided by the TA's.

Homework #1 [problem 1.14, 1.15, 1.17, 2.1, 2.4, 2.5] ( Sep. 30, Fri.), Solution(周明翰)
Homework #2 [problem 2.10, 2.12, 2.13, 2.17, 2.20, 2.22, 2.24, 2.27, 2.34, 2.46]( Oct. 18, Tue.), Solution(蔡松庭)
Homework #3 [problem 3.1, 3.3, 3.5, 3.13, 3.22, 3.25, 3.26, 3.33] ( Nov. 11, Fri.), Solution( 許智婷)
Homework #4 [problem 3.12, 3.21,3.23, 3.27, 3.36, 3.37, 3.38, others ] ( Nov. 29, Tue.), Solution(周明翰)
Homework #5 [Problem 4.2, 4.3, 4.6, 4.7, 4.9, 4.19, 4.26, 4.38]( Dec. 20, Tue.), Solution( 許智婷)
Homework #6 [Chapter 4: 11, 13, 17, 25, 27, 30, 40-(a)(b), 48, 49, 55]( Jan. 6, Fri.), Solution(蔡松庭)

Syllabus:

The first 5 chapters in Griffith will be covered
in this semester. More supplementary materials from the
references, including the history and applications, will be
provided alongside.

Course Log:

Sep.13(Tue.): Introduction, wave function and intrepretation, standard deviation, normalization [1.1,1.2,1.3,1.4 ]
Sep.16(Fri.): Momentum, operators, Ehrenfest's theorem, uncertainty principle [ 1.5, 1.6]
Sep.20(Tue.): Gaussian wave function, time-dependent Schrodinger Eq. [2.1]
Sep.23(Fri.): Infinite square well [2.2]
Sep.27(Tue.): Harmonic oscillator- algebraic method [2.3.1]
Sep.30(Fri.): Harmonic oscillator- diff. eq. method [2.3.2] 收HW1
Oct.4(Tue.): SHO and free particle
Oct.7(Fri.): Free particle [2.4]
Oct.11(Tue.): Bound states and Scattering states, delta-function potential [2.5]
Oct.14(Fri.): finite depth square well [2.6]
Oct.18(Tue.): review and summary of what we have learnt so far 收HW2
Oct.21(Fri.): Midterm-1
Oct.25(Tue.): Midterm problems, discussion, Mathematica (v6.0) Program
Oct.28(Fri.): matrix representation for operator, k-space Schrodinger equation
Nov.1(Tue.): hermitian operator, Dirac notation, linear vector space
Nov.4(Fri.): Hilbert space, Schmidt process, Schwarz inequality, Linear operator, adjoint operator
Nov.8(Tue.): Eigenvalue problem, projection operators and completeness
Nov.11(Fri.):N-site ring as an example for x basis, k basis, and wave function, Dirac normalizable 收HW3
Nov.15(Tue.): Momentum and Hamiltonian operator in x basis
Nov.18(Fri.): Uncertainty principle
Nov.22(Tue.): 2-state system
Nov.25(Fri.): more on 2-state system
Nov.29(Tue.): Stern-Gerlach Exp and Pauli matrices[4.4] 收HW4
Dec.2(Fri.): Midterm-2
Dec.6(Tue.): midterm problems and discussion
Dec.9(Fri.): 3D Schrodinger equation[4.1]
Dec.13(Tue.): infinity spherical well, spherical Bessel/Neumann function, Angular Momentum[4.3]
Dec.16(Fri.): More on angular momentum[4.3]
Dec.20(Tue.): Derive the Spherical Harmonics, H-atom ground state energy from uncertainty principle 收HW5
Dec.23(Fri.): H-atom [4.2]
Dec.27(Tue.): more on Spin, addition of angular momenta [4.4]
Dec.30(Fri.): Clebch-Gordan coeff. Spin-1 operator, rotation and angular momentum
Jan.3(Tue.): 2-particle systems [5.1]
Jan.6(Fri.): final review 收HW6
Jan. 10 (Tue.): Final Exam

since June 24, 2011
rec2rec