15-07 The Hubble Law

• The Hubble law
   
  • In 1929, Edwin Hubble published his discovery of the relation between red shifts and distances of galaxies within 2 Mpc, later in 1931 extended to 32 Mpc.
    
    
    
    
    
     
  • What is measured is the red shift of lines in the spectrum of distant galaxies.
    That red shift is "interpreted" as a receding velocity.
    (Chapter 5, General Astronomy (I))
     
    z = (λ₁-λ₀)/λ₀ = (1+β_r)/(1-β²)^1/2 - 1
     
    β = [(z+1)²-1]/[(z+1)²+1]    for β = β_r
    
    
     
    z ~ β_r    for β << 1
     
  • The Hubble law

    v (= cz) = Hd
     
    This is an empirical law, which concerns galaxies in other galaxy clusters, or, to put it in another way, which is about galaxy clusters.
    The Hubble law does not apply within a galaxy cluster.

• H, the Hubble constant (or better called the Hubble parameter), is difficult to determine.
  Its value ranges from 50 km/sec/Mpc ~ 100 km/sec/Mpc.
  A recently often quoted value is 70 km/sec/Mpc.
  
  However, there is a so-called Hubble constant tension among different measurements:
  
  
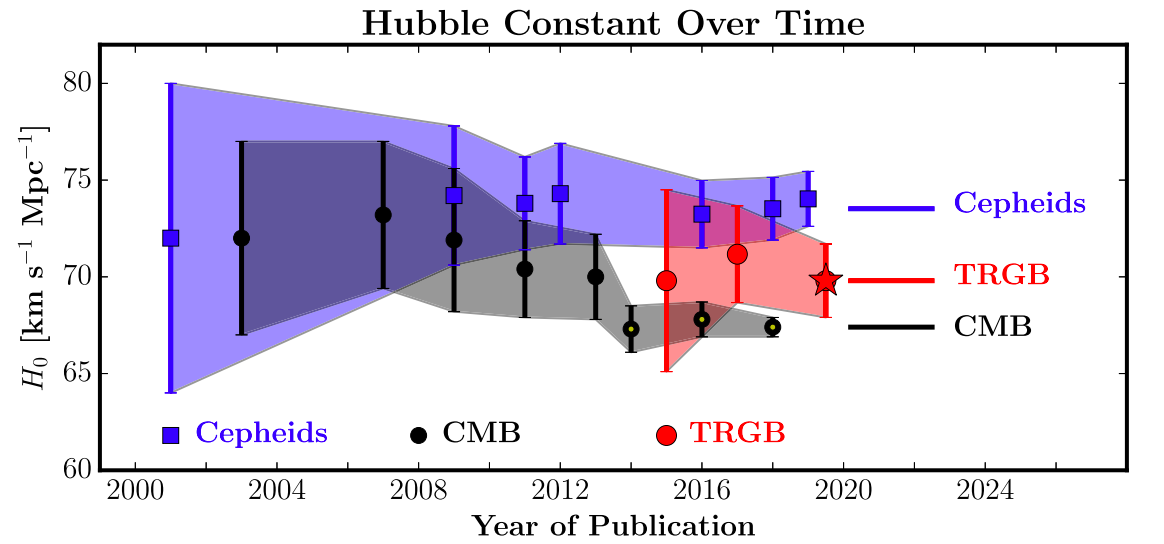
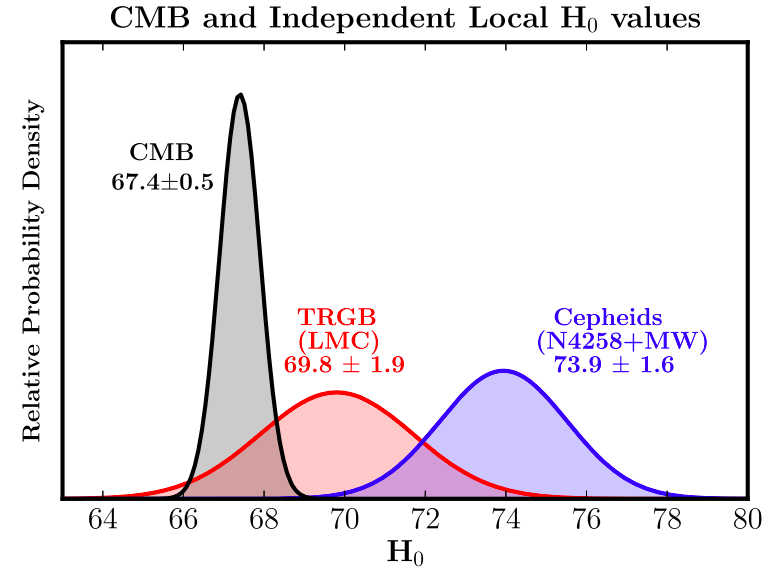
  [Hubble constant seems to be different for local (recent) and far-away (long time ago) universe. Figures are taken from Freedman et al. 2019, ApJ 882, 34. 'Cepheids' is for methods using Cepheid-calibrated SN Ia and 'TRGB' for TRGB-calibrated SN Ia. TRGB stands for 'tip of red giant branch'.]
  
  (There is an alleged indication that the Hubble constant is not isotropic: the universe expands faster in a certain direction and slower in another; see Migkas et al. 2020, A&A 636, A15.)
  
  (Check Hubble's original value: 1/1790 km/sec/pc ~ 560 km/sec/Mpc)
  
  [Hubble 1931 paper]
  
   
• With a Hubble constant, the Hubble law can be used to determine the distance, given an observation-determined redshift.
  The distance is very often expressed like d = 90 Mpc h^-1, where h=H/100 km/sec/Mpc
   
• An expanding universe!
   
• Not all galaxies are moving away from us.
  Galaxies have their own local, intrinsic motion.
  M31 is actually approaching us, blue-shifted.
  At larger distance, the 'Hubble flow velocity' dominates over galaxies' local, intrinsic motion in a cluster.
   
• The Hubble law does not hold any more at a very large distance!
  
  It is only valid for z << 1. For larger z, the relation between z (the redshift) and d (the distance, to be determined with other methods) is not well measured. Different cosmological models predict different d-z relations. Astronomers often simply use z, rather than d or the so-called 'look-back time', to refer to a distant object.
  
  
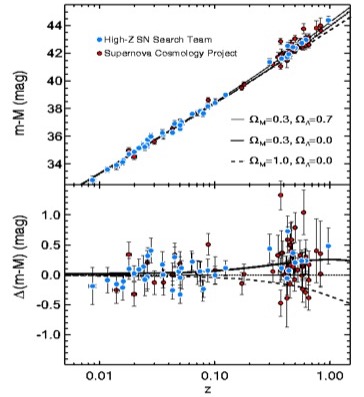
  [The SN Type-Ia d-z diagram; the distance module "m-M" in the ordinate (y-axis) corresponds to the (luminosity) distance plotted in a logarithmic scale. ]